High School Research at Jefferson Lab

Numerical Experiment on Nonlinear Particle Dynamics

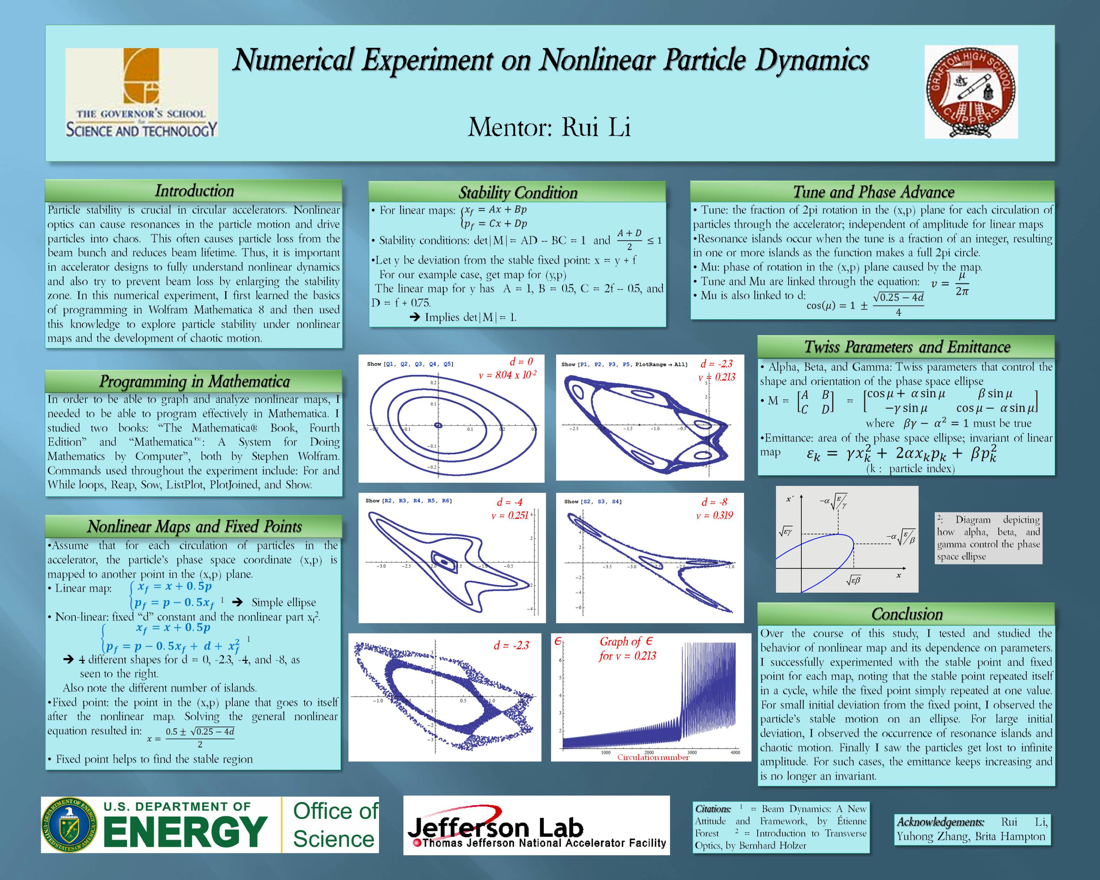
In order to understand the chaos that originates from the particles scattering in the accelerator beam, I needed to be able to map degree of freedom functions in Mathematica to see how the maps behave. Therefore, I spent a considerable amount of time first learning how to program basic functions in Mathematica through two different textbooks, then began to study linear functions as a pre-cursor to their nonlinear counterparts. Afterwards, I began to graph nonlinear degree of freedom cases, as given by the book "Beam Dynamics: A New Attitude and Framework", by Etienne Forest. As I experimented more with nonlinear maps, and saw how they changed with different values, I also learned about the various characteristics/parameters that make up these maps, such as fixed point, tune, alpha/beta/gamma, and epsilon. Thus, through the use of graphing in Mathematica and studying from excerpts in "Beam Dynamics: A New Attitude and Framework", I was able to gain a much more full understanding of the chaos that takes place in the accelerator beam.