Undergraduate Research at Jefferson Lab

Coding and Analyzing Hamiltonian Monte Carlo Algorithm Variants for Target Posterior Distributions

Student: Georgios Vassilakopoulos

School: Old Dominion University

Mentored By: Kostas Orginos

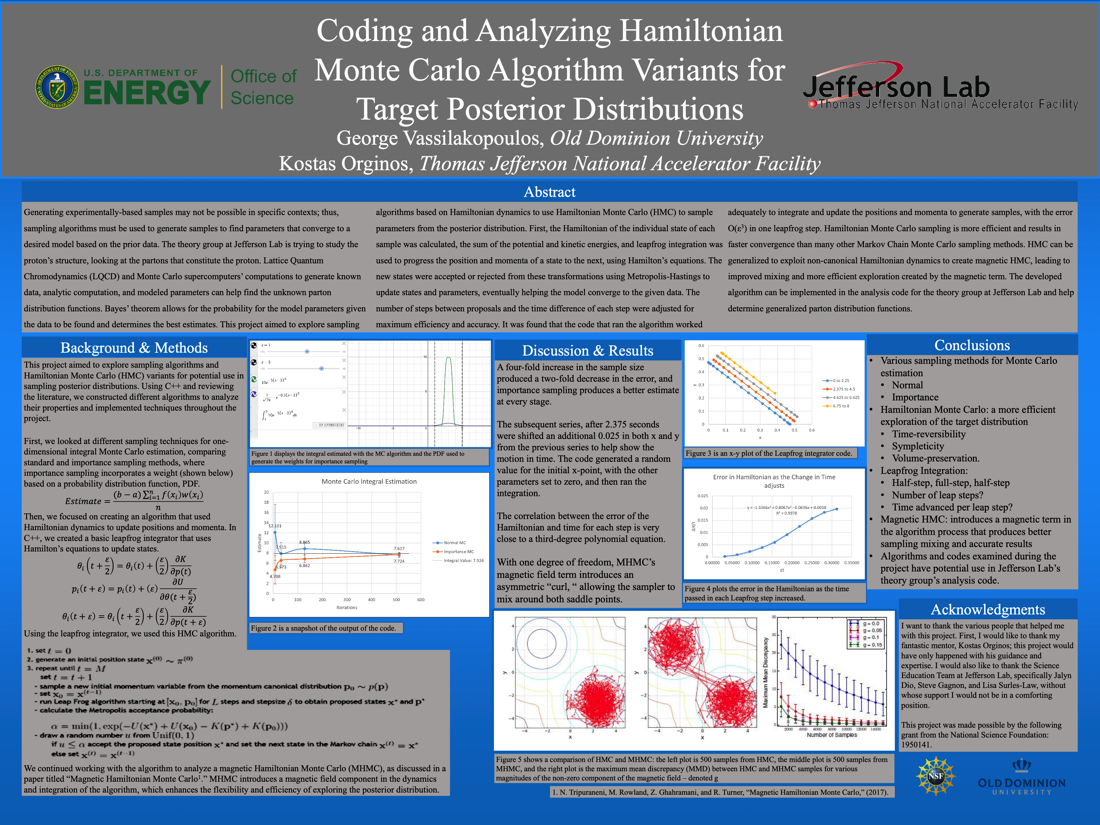
Sampling algorithms can generate samples to find parameters that converge to an unknown distribution. Jefferson Lab's theory group studies the proton's structure by generating known data, analytic computation, and model parameters and applying it to Bayes' theorem to determine parton distribution functions. This project explored sampling algorithms based on Hamiltonian dynamics to use Hamiltonian Monte Carlo (HMC) to sample parameters from the posterior distribution. Leapfrog integration progressed the position and momenta of states to the next. Metropolis-Hastings' acceptance/rejection was applied to proposed states, converging the samples to the target distribution. It was found that the code's algorithm worked adequately to integrate and update the dynamics to generate samples, with the error O(ε³) per leapfrog step. HMC sampling is more efficient than other methods. It can be generalized to exploit non-canonical Hamiltonian dynamics to create magnetic HMC with improved mixing and exploration. The developed algorithm can be implemented in the analysis code for the theory group at Jefferson Lab.